Term Rewrite, E-Graph, and?

Term Rewrite System (TRS)

More about TRS

  • Termination: no infinite sequences of rewrites
    • terminates?
    • reduction ordering? s.t.
  • Confluence: the order of rewrites doesn’t matter
  • Completion: transform equations into confluent TRS
  • Stategies: controls the applications of term rewriting

Optimizations as Rewrite Strategies

type Strategy[P] = P => RewriteResult[P]
RewriteResult[P] = Success[P](P)
                 | Failure[P](Strategy[P])
type Traversal[P] = Strategy[P] => Strategy[P]

def ‘@‘[P](s: Strategy[P], t: Traversal[P]) = t(s)
def outermost: Strategy[Rise] => Traversal[Rise] = 
  pred => s => topDown(pred ‘;‘ s)
// tiling 32x32, nest level 2 in ELEVATE
(tile(32,32) ‘@‘ outermost(mapNest(2)))(mm)
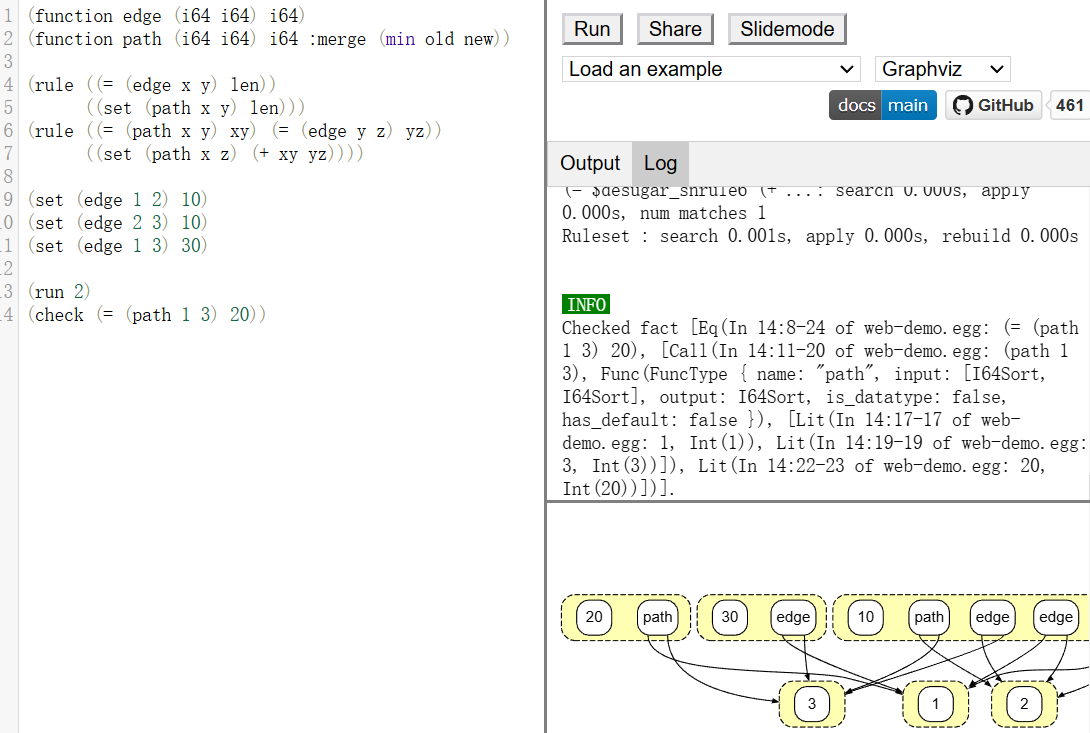
Achieving High-Performance the Functional Way: A Functional Pearl on Expressing High-Performance Optimizations as Rewrite Strategies, ICFP 2020. https://doi.org/10.1145/3408974

E-graph

E-graph?

  • first used in verification
  • equality with uninterpreted functions
  • if , ???

QF-EUF: quantifier-free equality with uninterpreted functions

What is an e-graph?

An e-graph is a tuple , where:

  • Hashcons is a map from e-nodes to e-class ids.
  • A union-find data structure stores equivalance retions e-class ids.
  • E-class map maps e-class ids to e-classes. All equivalent e-class ids map to the same e-class.

Operations in e-graph

  • Mutation
    • add: takes an e-node, (insert an e-class if not exist), returns the e-class id;
    • merge: unions two e-class ids;
  • Query
    • find: canonicalizes e-class id with union-find;
    • ematch: performs e-matching for finding patterns in the e-graph.

More about e-matching

  • input: a pattern term with variables
  • output: a list of tuples
    • is a substitution of variables to e-class ids
    • is represented in e-class
  • example: e-matching 
for e-class c in e-graph E:
  for f-node n1 in c:
    subst = {root ↦ c, α ↦ n1.child1}
    for g-node n2 in n1.child2:
        if subst[α] = n2.child1:
            yield subst

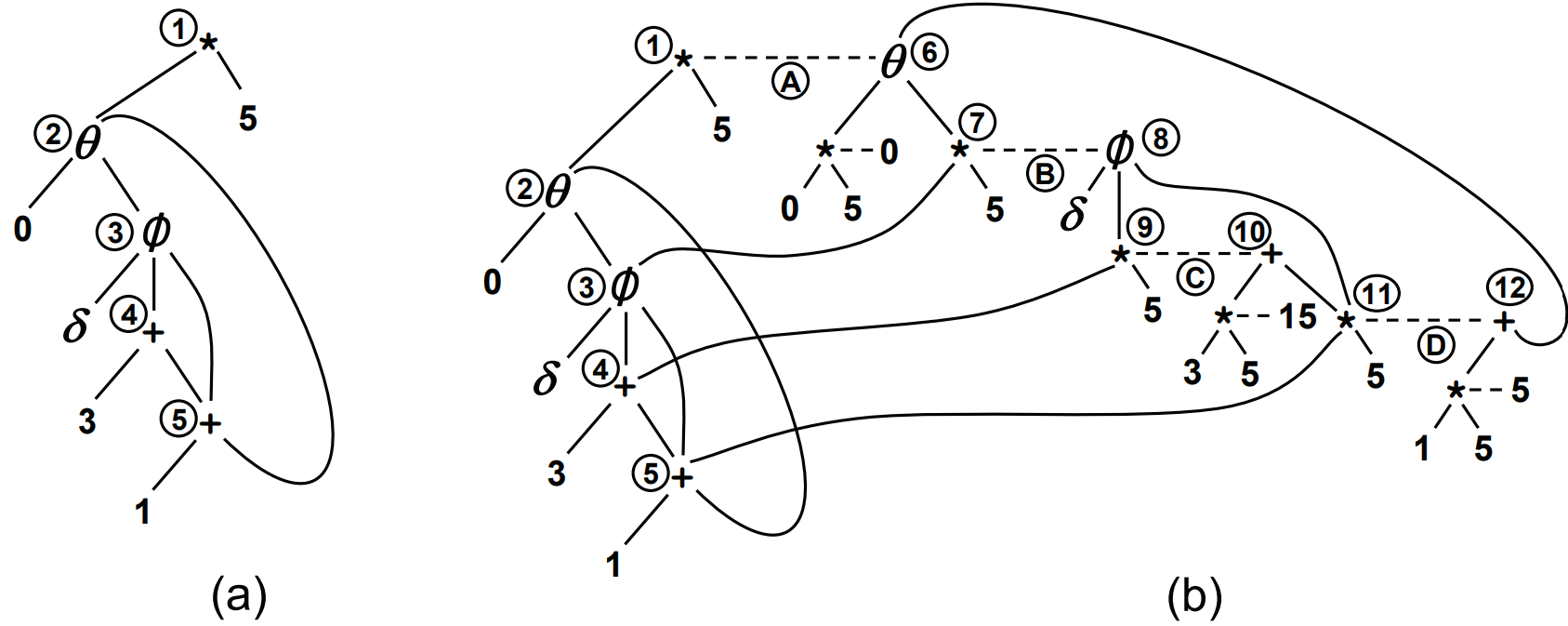
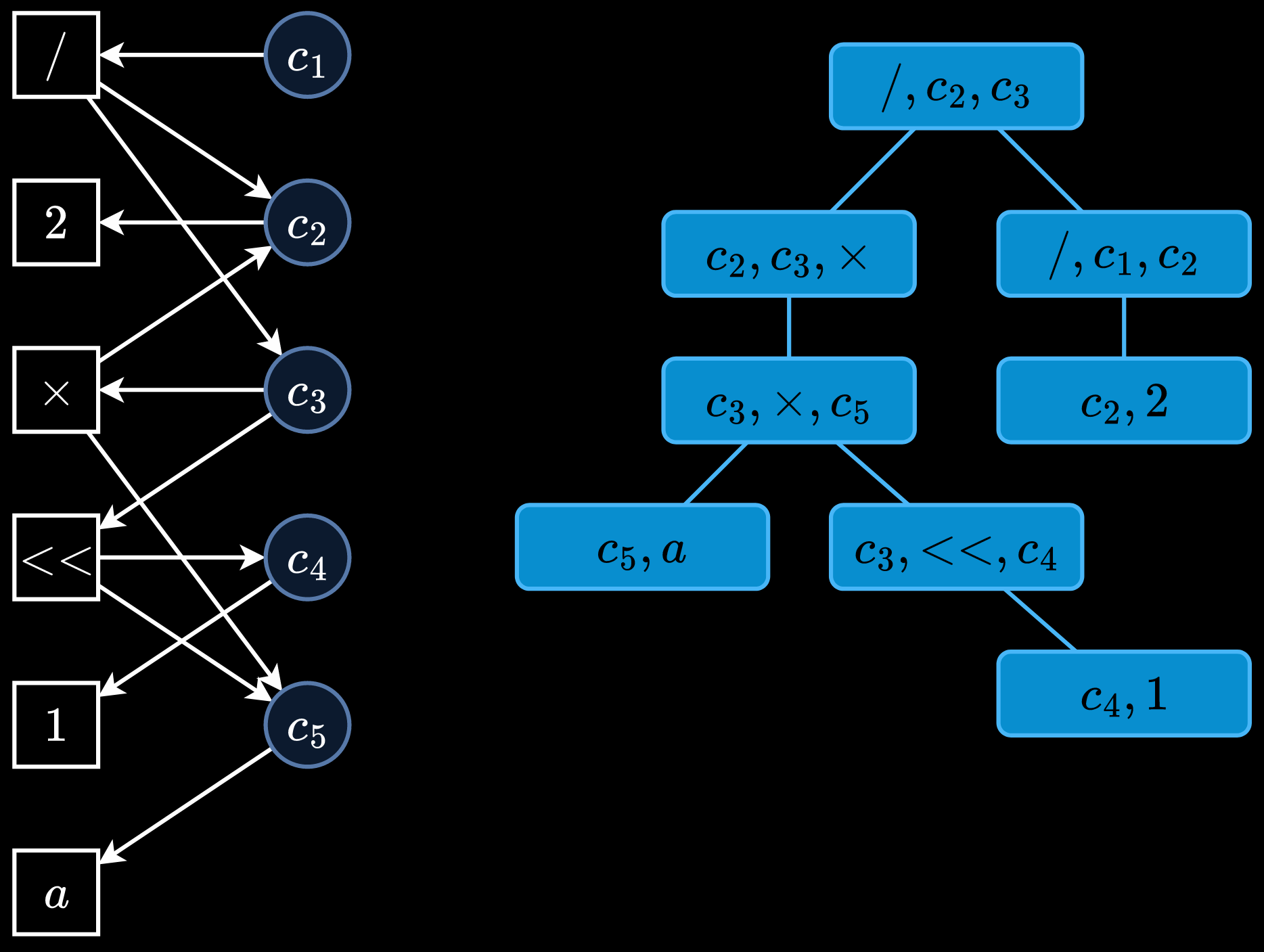
Rewriting over e-graph

  • rewrite:
  • ematch to find tuples , represents
  • for each , merge(, add())



(Div (Mul a two) two)


(Div (Shl a (Num 1)) two)
; (Div (Mul a two) two) still exists

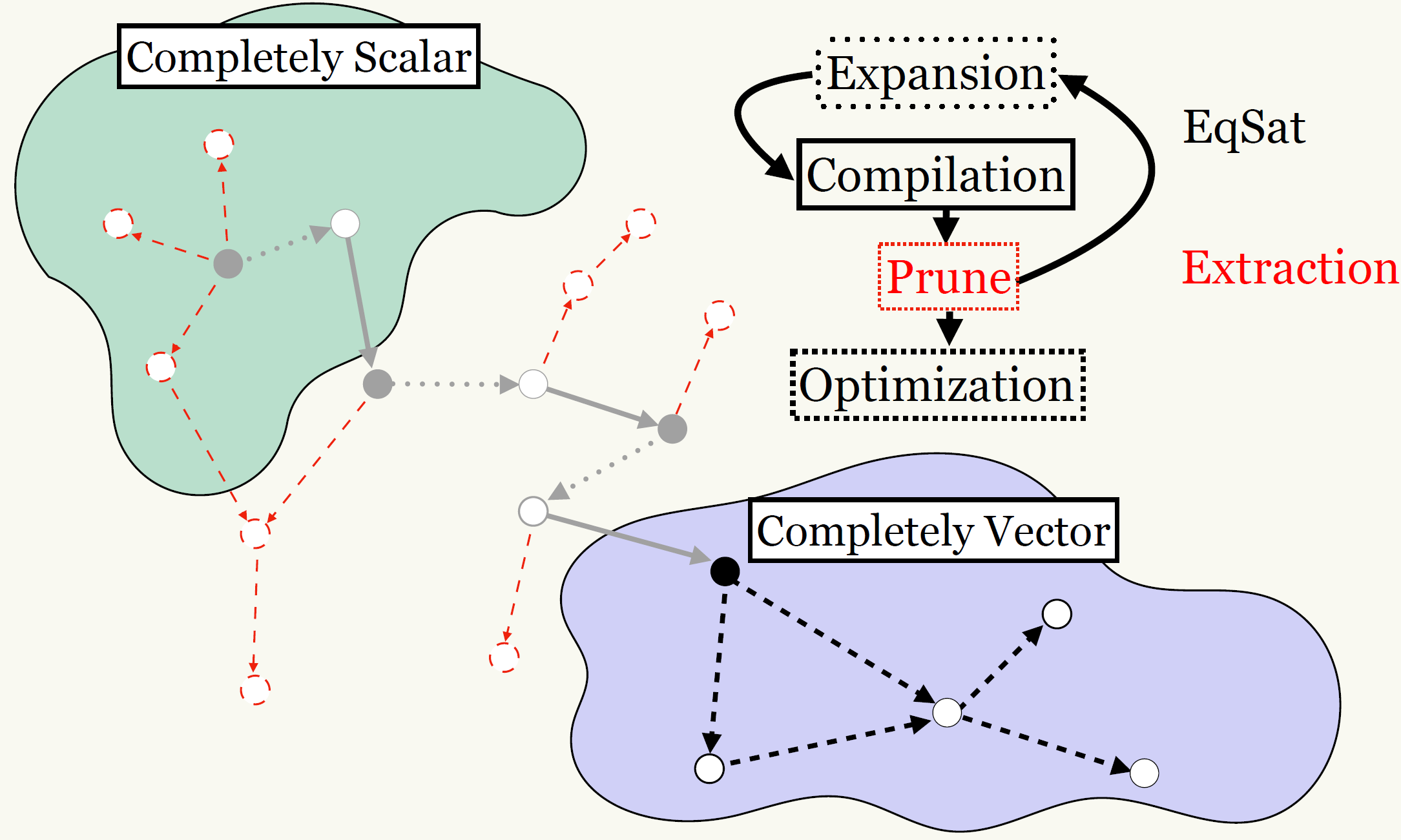
Equality Saturation: why? and how?

  • Term rewriting is destructive -- forgets LHS
    • Phase ordering problem: when to apply which?
  • EqSat: apply all rewrites, keeping track of every discovered expression, in e-graph.

def equality_saturation(expr, rewrites): 
  egraph = initial_egraph(expr) 
  while not egraph.is_saturated_or_timeout(): 
    for rw in rewrites: 
      for (subst, eclass) in egraph.ematch(rw.lhs): 
        eclass2 = egraph.add(rw.rhs.subst(subst)) 
        egraph.merge(eclass, eclass2) 
  return egraph.extract_best()

EqSat + extraction

(rewrite (Mul a two) 
         (Shl a (Num 1)))
(rewrite (Div (Mul %x %y) %z) 
         (Mul %x (Div %y %z)))
(rewrite (Div %x %x) one)
(rewrite (Mul %x one) %x)


(extract (Div (Mul a two) two))

; outputs:
;   (Var "a")

So what's egg?

first general-purpose, reusable implementation of e-graphs and equality saturation
MAKES E-GRAPH GREAT AGAIN

What's new?

  • rebuilding for amortized invariant maintenance
    • fast EqSat: 20.96× speedup. GPU? ray-tracing-alike?
  • e-class analysis: abstract interpretation in e-graph
    • a domain , value for each e-class
    • conditional rewrites: only if

Egg in action: Herbie

Herbie uses e-graphs for algebraic simplification of mathematical expressions

The egg backend is over 3000× faster than Herbie’s initial simplifier

Find and fix floating-point problems:

sqrt(x+1) - sqrt(x) 
  ->  1/(sqrt(x+1) + sqrt(x))

accuracy: 53.1% -> 99.7%

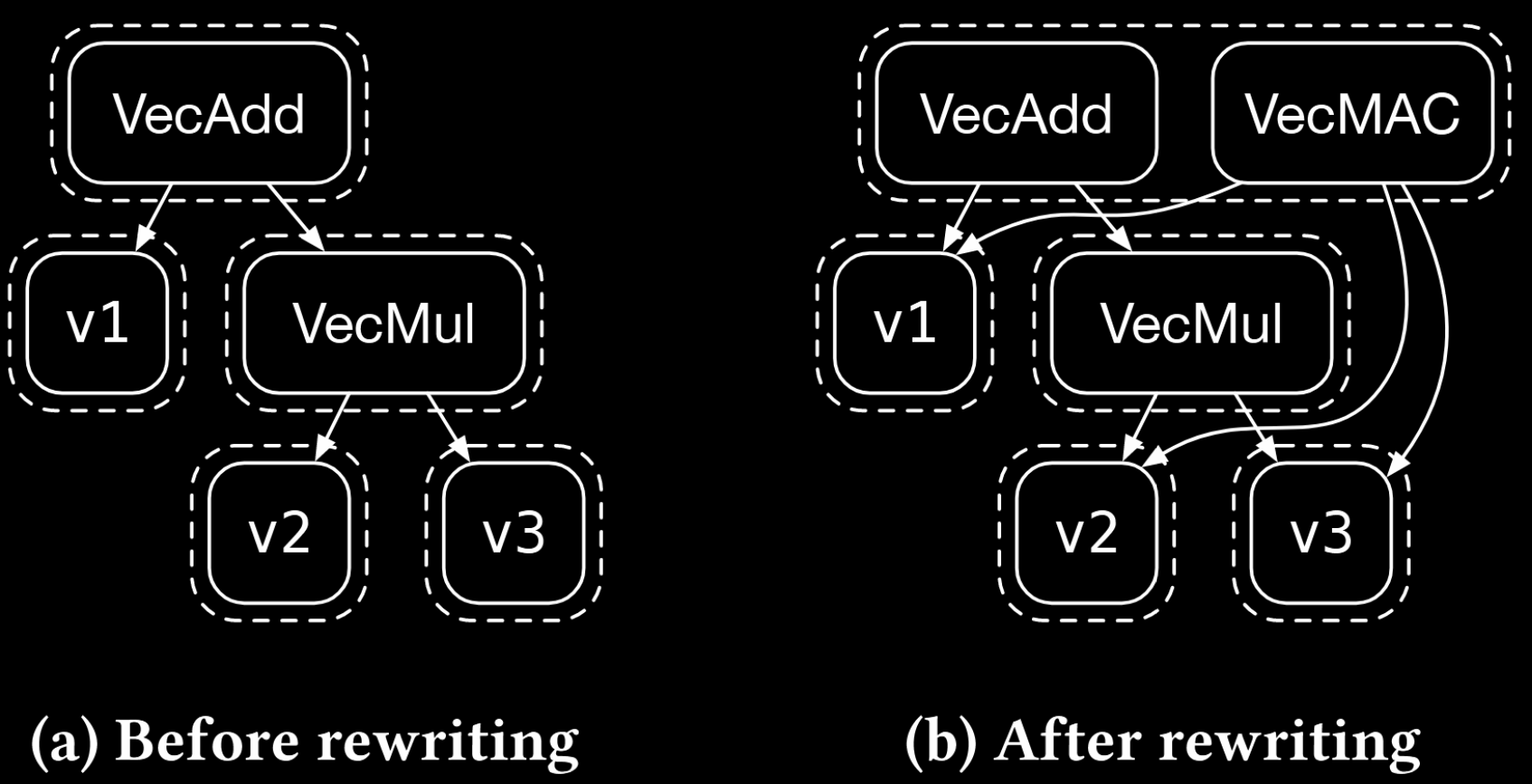
Egg in action: datapath optimization

Abstract domain:

Constraint? Context!
Colored e-graph

Automating Constraint-Aware Datapath Optimization using E-Graphs. DAC 2023,doi: 10.1109/DAC56929.2023.0247797.

More about extraction

The target e-class represents
, , , ...
which one to extract?
pick the smallest (cheapest) one

  • Valid extraction:
    1. if we extract an e-class, we have to extract at least one of its members
    2. if we extract an e-node, we must also extract all of its children
  • Optimal extraction:
    • a valid extraction that includes all the target e-classes and has the smallest total cost

ILP extraction

Variables:
for each e-node

Objective:

Constraints:

  • Root constraints:

  • Class constraints

for each child of

  • Acyclic constraints

Treewidth extraction for sparse e-graphs

Intuition: 
when treewidth is small, every bag is small, 
and we can enumerate extraction within each bag; 
and thanks to the cut property, 
we can conduct dynamic programming over bags.

But, decomposition is slow!

Extraction in E-Syn

E-GRAPH REWRITING FOR LOGIC SYNTHESIS

  • Regression: XGBoost model to fit the area and delay cost from the AST of a Boolean expression
    • cost model is not linear or monotonic
  • Pool extraction: heuristics + random sampling + apply XGBoost model
    • tradeoff between local heuristics and ILP
    • need ~100+ samples

E-graph for compiler

No-egg rewrite-based optimizer

Phase ordering problem is SEVERE! CF is HARD!

ægraphs[slide]

  • accepted in Cranelift compiler
    • part of Wasmtime
  • Solution
    • e-graph + CFG skeleton
    • persistent immutable data structure
  • Restricted but fast!

E-graph for instruction selection

Diospyros

low-level instr. as e-nodes
fully-unrolled kernel
EqSat TIMEOUT!
e.g. MatMul 8*8*8

Isaria (using Ruler)

Even with phasing, Isaria is slower than Diospyros!

E-graph for instruction finding

Isaria makes adding a new instruction easy

(match inst
; ...
  [(sqrt-add e1 e2) (+ (sqrt e1) e2)]
  [(vec-sqrt-add v1 v2) 
    (for/list ([e1 v1] [e2 v2])
      (sqrt-add e1 e2))]
)

Rewrites are auto-generated!

I fail to run Isaria...

What instructions? Babble

Beyond EqSat?

Egglog = Egg + Datalog

[tutorial] [demo]

Egglog is a powerful language!

  • rich features:
    • multi-patterns, incrementality
    • functions + equality
    • ...

[demo] is a good place to try ideas!

- Strategies encode program transformations - Rewrite rules are strategies - Strategies as compositions - Use traversals to describe at which exact location a strategy is applied

Suppose $\mathcal{A}[x]=[-3,3]$, then $\mathcal{A}[\texttt{ASSUME}(x,x>0)]=[1,3]$

![bg right:40% 100% saturate:2.0 opacity:.5](treewidth-decomp.png)

[Babble](https://dl.acm.org/doi/10.1145/3571207): library learning modulo theories

### What we need? > instruction finding from domain of applications - program rewrites: [eggcc](https://github.com/egraphs-good/eggcc)? [jlm](https://github.com/phate/jlm)? what else? - tractable EqSat: - pruning ([Isaria](https://dl.acm.org/doi/10.1145/3617232.3624873))? guiding ([egg-sketch](https://dl.acm.org/doi/10.1145/3632900))? - learn instruction: - what to learn? acceptable instr.? cost model? - how to learn? [Babble](https://dl.acm.org/doi/10.1145/3571207)? - more efficient extraction?